Rotations have some special considerations more than the other transformations. Some of the issues that you need to understand when animating rotations are the transformation node in which you can manipulate and key rotations (see Manipulation Modes versus Transformation Values), Euler versus quaternion rotations, gimbal lock, and continuous rotations.
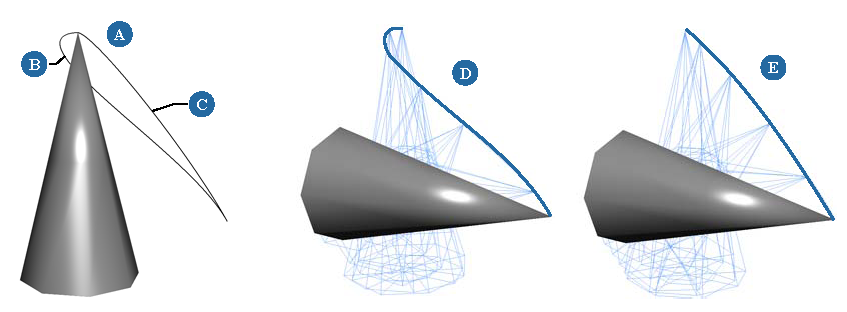
When you animate rotations in Softimage, you normally use three separate function curves that are connected to the X, Y, and Z rotation parameters. These three rotation parameters are called Euler angles. Euler angles are simple to understand and control because each rotation axis is evaluated in a set order. This process is known as Euler interpolation.
Euler interpolation works well when the axis of interpolation coincides with one of the XYZ rotation axes, but is not as good at interpolating arbitrary orientations. For example, it may be difficult to get smooth interpolation when animating the orientation of either a ball joint, such as a shoulder, or of a tumbling object whose animation is not around one of the XYZ axes.
Euler angles can also suffer from gimbal lock, which is the phenomenon of two rotational axes aligning with each other so that they both point in the same direction. This happens because the XYZ axes are not independent, so changing one axis can affect the preceding ones. For example, if you apply a 90-degree rotation to the Y axis, it causes the X axis to coincide with the Z axis so that rotating in X and Z has the same effect.
Gimbal lock can be compensated for by changing the order in which the rotation axes are evaluated (by default, it's XYZ), which changes where the gimbal lock occurs (see Changing the Bones' Order of Rotation).
Quaternion interpolation provides a way to overcome these limitations and provide smooth interpolation with any sequence of rotations. With this type of interpolation, the XYZ angles are treated as a unit to determine an object's orientation so they are not restricted to a particular order of rotation axes. Quaternions interpolate the shortest path between two rotations.
You can create quaternion fcurves in Softimage by either setting quaternion keys or converting Euler to quaternion function curves. These curves are true quaternion curves, but are drawn as three separate fcurves (as Euler fcurves are represented) in the fcurve editor to make them easier to edit.
Because the three fcurves are an approximation of the underlying quaternion fcurve, the displayed values may have discontinuities where the XYZ angles change abruptly. This is only a display artifact and does not affect the interpolation. You can usually minimize these discontinuities by making the fcurve rotations continuous (see Making Rotations Continuous).
When you set, delete, or move a key on a quaternion fcurve, the change appears on all three fcurves because the entire rotation is being interpolated by the quaternion fcurve.
You can edit quaternion fcurves in both the fcurve editor and the dopesheet as you would normal fcurves. However, quaternion fcurves do not have tangents for editing fcurve slopes as typical fcurves do, but instead use special parameters to edit the fcurve's interpolation (see Editing Quaternion Function Curves).
It's a simple process to convert from Euler to quaternion rotations and back again. However, as with most conversions, information is changed in the process. This is because quaternion fcurves store one key for the entire XYZ rotation value.
When you convert Euler fcurves to quaternion fcurves, a quaternion key is added for each key in the XYZ fcurves. For example, if there is a key at frame 5 for the Euler rotation X parameter but not Y and Z, a quaternion key is generated for each rotation parameter by sampling the XYZ values at frame 5.
Also, any slope (tangent) information on the Euler fcurves is lost when converting to quaternions.
Select an object with Euler rotation fcurves and choose Animation 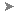 Convert Euler Rotation to Quaternion from the Animation panel.
Convert Euler Rotation to Quaternion from the Animation panel.
Edit the timing and interpolation of the quaternion curves in the fcurve editor using the Quaternion Key controls — see Editing Quaternion Function Curves.
Setting keys to create quaternion rotation fcurves is the same process as for setting Euler rotation fcurves except that you can key quaternion rotations only an object that already has rotation fcurves (either Euler or quaternion). When you set and key the object's rotation as quaternion, you get a smooth interpolation.
Select an object with either Euler or quaternion rotation fcurves.
Choose Animation  Convert Euler Rotation to Quaternion from the Animation panel.
Convert Euler Rotation to Quaternion from the Animation panel.
If you select an object that already has Euler rotation fcurves, the curves are simply converted to quaternion.
Key rotations as usual and the resulting fcurves will be quaternion.
Setting keys for one rotation axis creates corresponding keys on the other two rotation axes.
Edit the timing and interpolation of the quaternion curves in the fcurve editor using the Quaternion Key controls — see Editing Quaternion Function Curves.
When you animate rotations 360 degrees or more, there may be problems with the rotations flipping or "spiking" when the values jump between equivalent but discontinuous numbers; for example, you're rotating a wheel 360 degrees in Y, and it goes 180 degrees in the correct direction but then rotates backwards to its original starting value.
By making a rotation fcurve continuous, the flipping is eliminated. If two keys on the fcurve have a gap of more than 180 degrees, the second key is offset by 180 degrees so that the object's rotation continues in the same manner.
You may want to make rotations continuous if you're planning to stretch, mix, or manipulate the animation as an action in the animation mixer.
If you want to process more than one rotation fcurve at a time, you can choose the Make Rotation Keys Continuous command from the Animation panel. This command processes all rotation curves on an object together as a complete orientation instead of individual X, Y, and Z rotation function curves.
This command also processes the local and global rotation keyframes on the selected objects to minimize the change between successive Euler angle rotation keyframes, making the values continuous between keys.
 Except where otherwise noted, this work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
Except where otherwise noted, this work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License