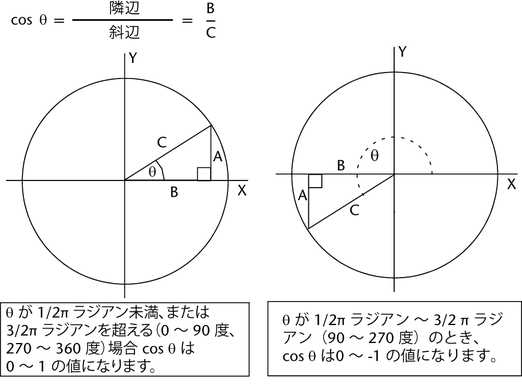
この比率は、三角形の大きさではなく角度の大きさだけに応じて変化します。この比率が角度の余弦と呼ばれます。
引数を一定の割合で増減させると、cos 関数も一定の割合で、1 ~ -1 の範囲内で増減させた値を返します。これはアトリビュート値をリズミカルに振動させる場合に便利です。
cos 関数は sin 関数と似ていますが、ちょうど 90 度(2/π)だけ位相がシフトした値を返します。
cos 関数と sin 関数の循環的な特性を利用する方法については、sin を参照してください。
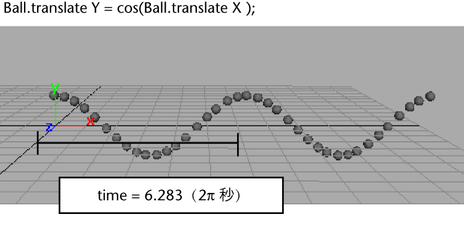
Ball の動きを余弦波形でアニメートする場合は、次のようなエクスプレッションを使用します。
Ball.translateX = time; Ball.translateY = cos(Ball.translateX);
Ball はワールド座標の原点から出発し、長くなるアニメーション時間(time)によって設定される速度で X 軸方向に移動します。また、Ball は cos 関数の戻り値に従って循環的に上下に(Y 軸に沿って)移動します。cos 関数の引数には移動 X(Translate X)アトリビュートの値(間接的には time の値)が渡されています。
time が 0 から 6.283 秒に長くなるに従って、cos 関数は 1 ~ -1 の間で少しずつ大きくなり、1 に戻る値を返します。6.283 という値は π の 2 倍です。
time が 6.283 秒を超えた後は、同じサイクル パターンが 6.283 秒を周期として繰り返されます。
sin 関数を使用して同じエクスプレッションを作成すると、次のようになります。
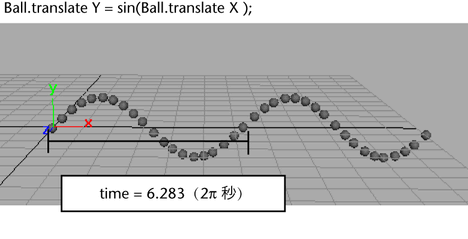
cos 関数のカーブと sin 関数のカーブは互いに 1.571 秒(π/2 秒)だけ前後にずれていることが分かります。