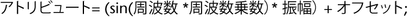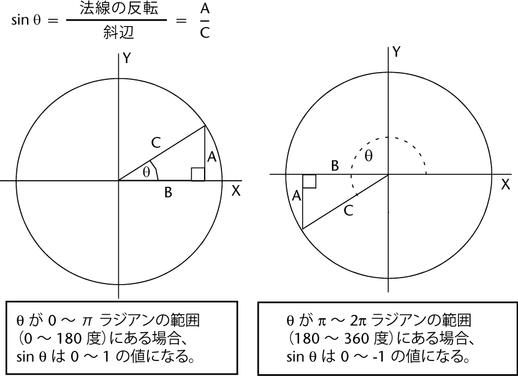
この比率は、三角形の大きさではなく角度の大きさだけに応じて変化します。この比率が角度の正弦と呼ばれます。
引数を一定の割合で増減させると、sin 関数も一定の割合で、-1 ~ 1 の範囲内で増減させた値を返します。これはアトリビュート値をリズミカルに振動させる場合に便利です。
たとえば、sin 関数を使用して次のような操作を実行することができます。
Ball.translateY = sin(Ball.translateX);
この文は、Ball の移動 Y(Translate Y)に移動 X(Translate X)の正弦を代入します。Ball を X 軸に沿ってドラッグすると、その移動 Y 位置が上下方向に循環的に移動します。
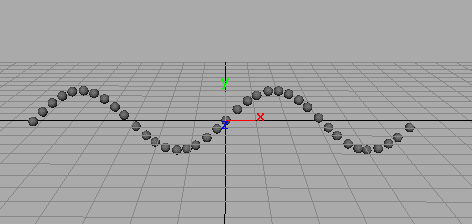
例 2のパスに沿って Ball をアニメートするには、次のようなエクスプレッションを使用します。
Ball.translateX = time; Ball.translateY = sin(Ball.translateX);
Ball はワールド座標の原点から出発し、長くなるアニメーション時間(time)によって設定される速度で X 軸方向に移動します。また、Ball は sin 関数の戻り値に従って循環的に上下に(Y 軸に沿って)移動します。sin 関数の引数には移動 X の値(間接的には time の値)が渡されています。
time が 0 から 6.283 秒に伸びるに従って、sin 関数は 0 ~ 1 の間で少しずつ大きくなり、1 になると少しずつ小さくなって -1 に戻る値を返します。-1 に戻ると、再び少しずつ大きくなって 0 に戻る値を返します。6.283 という値は π の 2 倍です。結果として S を横向きにしたような形の動きになります。
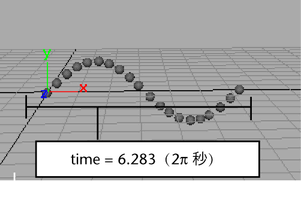
time が 6.283 秒を超えた後は、同じ S 字形サイクル パターンが 6.283 秒を周期として繰り返されます。
上下の振幅を大きくして Ball をアニメートするには、次のようなエクスプレッションを使用します。
Ball.translateX = time; Ball.translateY = sin(Ball.translateX) * 2;
sin(Ball.translateX) に 1 より大きい値を掛けると、正弦波形の振幅が大きくなります。振幅とは、波形の最大値と最小値の差を 2 で割った値です。
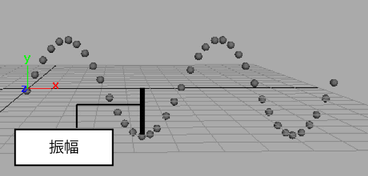
正弦波形の振幅を小さくするには、sin(Ball.translateX) に 1 より小さい値(0.5 など)を掛けます。
正弦波形の周波数を大きくするには、次のようなエクスプレッションを使用します。
Ball.translateX = time; Ball.translateY = sin(Ball.translateX * 2);
Ball.translateX に 1 より大きい値を掛けると、正弦波形の周波数が増加します。周波数とは、波形が 1 回サイクルするのに必要な時間です。
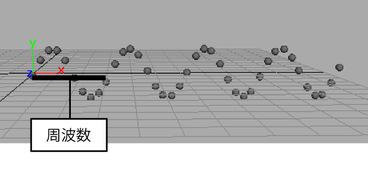
正弦波形の周波数を小さくするには、sin(Ball.translateX) に 1 より小さい値(0.5 など)を掛けます。この値は、正弦パターンの周波数を乗算(または除算)するため、周波数乗数と呼ばれます。
次のようなエクスプレッションを使用して、正弦波形を Y 軸に沿って上方向にオフセットします。
Ball.translateX = time; Ball.translateY = sin(Ball.translateX) + 2;
sin(Ball.translateX) に 2 を加算すると、波形が Y 軸に沿って上方向に移動します。負の値を加算すると、波形が Y 軸に沿って下方向にシフトします。

次のエクスプレッションでは、1 つの文の中で周波数乗数、振幅、オフセットを組み合わせて、正弦波形を調整しています。
Ball.translateX = time; Ball.translateY = (sin(Ball.translateX * 2) * 2) + 2;

次の図に、正弦波形の周波数乗数、振幅、上下シフト(オフセット)を設定している値を示します。
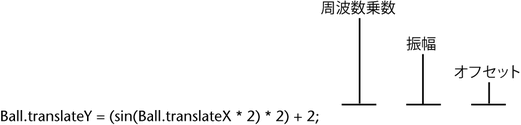
正弦波形の調整に使用できる各ファクタの一般公式は、次のとおりです。