Free-Form Surface Geometry
Free-form surfaces are polynomial patches of any degree up to
twenty-one. [11] Supported basis types
include Bézier, Taylor, B-spline, cardinal, and basis-matrix form. Any
type can be rational or non-rational. Patches can be explicitly or
automatically connected to one another, or may be defined to
contain explicitly defined points or curves in their approximation. Various approximation
types including (regular) parametric, spatial, curvature-dependent,
view-dependent, and combinations of these. mental ray 3.1 also
introduces fine approximation,
which can generate microtriangle tessellations very efficiently.
Surfaces may be bounded by a trimming curve, and may contain
holes.
Surface geometry, like polygonal geometry, is defined by a
series of sections. An object containing only surface geometry
follows this broad outline:
object "object_name"
[ visible [ on|off] ]
[ shadow [ on|off] ]
[ shadowmap [ on|off] ]
[ trace [ on|off] ]
[ reflection [ mode] ]3.4
[ refraction [ mode] ]3.4
[ transparency [ mode] ]3.4
[ select [ on|off] ]
[ tagged [ on|off] ]
[ caustic [ on|off] ]
[ globillum [ on|off] ]
[ face [ front|back|both] ]3.4
[ caustic [ mode] ]
[ globillum [ mode] ]
[ box [min_x min_y min_z max_x max_y max_z] ]
[ motion box [min_x min_y min_z max_x max_y max_z] ]
[ max displace value ]
[ samples min max ]
[ data null|"data_name" ]
[ tag label_numberint ]
[ basis list ]
group
vector list
vertex list
[ list of curves ]
surface
[ list of surface derivative requests ]
[ list of texture or vector surfaces ]
... # more surfaces
[ list of approximation statements ]
[ list of connection statements ]
end group
end object
Curves, surfaces, approximations, and connections may be
interspersed as long as names are defined before they are used. For
example, a curve must come before the surface it is trimming, and
an approximation must come after the surface to be approximated.
Texture and vector texture surfaces must always directly follow the
surface they apply to. The individual sections are:
- The basis list must be specified at the beginning of the
object definition, just before the group begins. Bases defined in
this section are referenced by name in the curve and surface
definitions to specify their degrees and types (Bézier,
B-spline, etc.).
- The vector list in the group is a list of (x, y,
z) vectors used to build control points later. This section is
the same as the vector section used to build vertices for polygonal
geometry.
- The vertex list that follows the vector list builds
control points out of the vectors. This also works like the vertex
list for polygonal geometry, except that no normals and texture
vertices can be defined here (no n, t,
d, or u statements may appear). Normals are
defined implicitly by the surface, and textures are defined by
texture surfaces instead as described below. Surface
derivatives are generated if derivative keywords are
present. Rational curves and surfaces specify additional weights at
each vertex reference (see below).
- Curves may be defined and used as trimming curves, hole curves, and special curves. This section is
optional; if no trimming curve is defined surfaces are untrimmed
and end at the boundaries specified by the ranges of the bases
used. Trimming a surface means to cut away portions that fall
outside an outer boundary curve; holes cut away portions inside the
hole curve. Special curves are curves that are always included in
the tessellation; they can be used to define features like sharp
creases that need to be tessellated consistently. Surfaces may also
be connected along trimming curves.
- The surface geometry list consists of surface
statements, much like polygonal geometry that consists of
p and c statements. A surface is defined by a
surface statement, optionally followed by surface derivative request statements
and one or more texture surface or vector surface
statements.
- Approximation statements give additional information
about how a surface and its trimming, hole, and special curves are
to be approximated with triangles. Various modes such as
parametric, regular parametric, curvature-dependent, and
view-dependent approximations can be selected, along with the
precision. If there are approximation statements in the
options statement (see
Options, Tessellation Quality above), they override any
approximation statements in the objects.
For a description of vector lists and vertex lists, refer to
page vector.
Bases
When surfaces and curves are
present within an object group,
it is mandatory that at least one basis has been defined within the object.
Bases define the degree and type of polynomials (denoted by
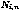 below) to be used in the description of
curves or surfaces. Curves and surfaces reference bases by name.
Every surface needs two bases, one for the U and one for the V
parameter direction. Both can have a different degree, but must
have the same type (for example, rational Bézier in U and
Cardinal in V is not allowed). There are five basis types:
below) to be used in the description of
curves or surfaces. Curves and surfaces reference bases by name.
Every surface needs two bases, one for the U and one for the V
parameter direction. Both can have a different degree, but must
have the same type (for example, rational Bézier in U and
Cardinal in V is not allowed). There are five basis types:
basis "basis_name" [ rational] taylor degreeint
basis "basis_name" [ rational] bezier degreeint
basis "basis_name" [ rational] cardinal
basis "basis_name" [ rational] bspline degreeint
basis "basis_name" [ rational] matrix degreeint stepsizeint basis_matrix
A parametric representation may be either non-rational or
rational as indicated by the rational flag. Rational
curves and surfaces specify additional weights at each control
point. This flag is optional; it can also be specified in the
curves and surfaces that reference the basis.
The degree specifies the degree of the polynomials used
in the description of curves or surfaces. Recall that the degree of
a polynomial is the highest power of the parameter occurring in its
definition. When bases of degree 1 are used control points are
connected with straight lines. Cardinal bases always have degree 3.
The degree and the type combined determine the length of the
parameter vector and
the number of control points needed for the surface. The meaning of
the parameter vector differs for the different basis types. This is
described in detail below.
The supported polynomial types for curves and surfaces are
bezier, bspline, taylor,
cardinal and matrix.
When a curve or surface is being evaluated and a transition from
one segment or patch to the next occurs, the set of control points
(the `evaluation window') used is incremented by the
stepsize. The appropriate stepsize depends on the
representation type expressed through the basis matrix and on the
degree.
Consider a curve with k control points  . If the curve is of degree n, then
n+1 control points are needed for each polynomial segment.
If the stepsize is given as s, then the
(1+i)th polynomial segment will use the control points
. If the curve is of degree n, then
n+1 control points are needed for each polynomial segment.
If the stepsize is given as s, then the
(1+i)th polynomial segment will use the control points
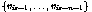 . For example, for Bézier curves
s=n, whereas for Cardinal curves s=1. For surfaces,
the above description applies independently to each parametric
dimension.
. For example, for Bézier curves
s=n, whereas for Cardinal curves s=1. For surfaces,
the above description applies independently to each parametric
dimension.
The basis_matrix specifies the basis functions used to
evaluate a parametric representation. For a basis of degree
n the matrix must be of size 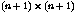 .
The matrix is laid out in the order
.
The matrix is laid out in the order 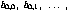
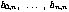 . Note that the generalization to the
rational case for all representations is admitted in all cases.
. Note that the generalization to the
rational case for all representations is admitted in all cases.
As an example, an object containing a nonrational Bézier
surface of degree 3 in one parameter direction and degree 1 in the
other parameter direction needs two bases defined at the beginning
of the object like this:
object "mysurface"
visible
basis "bez1" bezier 1
basis "bez3" bezier 3
group
...
The surface definition will reference the two bases by their
names, bez1 and bez3.
Surfaces
A surface specifies a name and a list of control points. For
both parametric dimensions it specifies a basis, a global parameter range, and a parameter list.
Optionally, it specifies surface
derivative requests, texture
surfaces, trimming curves,
hole curves, special curves and special points. Special curves and
points are included as edges and vertices in the approximation (triangulation) of the
surface.
surface "surface_name" "material_name"
"u_basis_name"range u_param_list
"v_basis_name"range v_param_list
hom_vertex_ref_list
[ derivative_request ]
[ texture_surface_list ]
[ surface_specials_list ]
If the enclosing object has the tagged flag set, a
label integer must be given instead of a material name (see page
tagged). This changes the first
line of the preceding syntax block to:
surface "surface_name"label_numberint
The bases used in the definition of the surface must have been
defined in the basis list of the object. They are referenced
by their basis_names. Their ranges consist of two
floating-point numbers specifying the minimum and maximum parameter
values used in the respective direction.
The parameter_lists in the basis specifications define
the number of patches of the surface and the number of control
points. For bases of the types taylor, bezier,
cardinal and matrix such a parameter_list
consists of a strictly increasing list of at least two
floating-point numbers. For bspline bases the
parameter_lists specify the knot vector. If the B-spline basis to be used is of degree
n, the knot vector  must have at
least q+1=2(n+1) elements. Knot values represent a monotone
sequence of floating-point numbers but are not necessarily strictly
increasing, i.e.
must have at
least q+1=2(n+1) elements. Knot values represent a monotone
sequence of floating-point numbers but are not necessarily strictly
increasing, i.e. 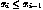 . Moreover, they must
satisfy the following conditions:
. Moreover, they must
satisfy the following conditions:
(1) 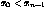 (2)
(2) 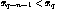 (3)
(3) 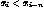 for
for 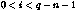 (4)
(4) 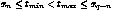
where 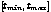 is the range over which the
B-spline is to be evaluated.
Equation (1) demands that no more than n + 1 parameters at
the beginning of the parameter list may have the same value.
Equation (2) is the same restriction for the end of the parameter
list. Equation (3) says that in the middle of the parameter list,
at most n consecutive parameters may have the same value. To
generate closed B-spline curves, it is often necessary to write a
parameter list where the first n and last n
parameters in the list produce initial and final curve segments
that should not become part of the curve; in this case equation (4)
allows choosing a start and end parameter in the range bounded by
the first and last parameter of the parameter list.
is the range over which the
B-spline is to be evaluated.
Equation (1) demands that no more than n + 1 parameters at
the beginning of the parameter list may have the same value.
Equation (2) is the same restriction for the end of the parameter
list. Equation (3) says that in the middle of the parameter list,
at most n consecutive parameters may have the same value. To
generate closed B-spline curves, it is often necessary to write a
parameter list where the first n and last n
parameters in the list produce initial and final curve segments
that should not become part of the curve; in this case equation (4)
allows choosing a start and end parameter in the range bounded by
the first and last parameter of the parameter list.
The number of control points per direction can be derived from
the number of parameters p, the degree of the basis
n, and the step size s. Their total number can be
calculated by multiplying the numbers taken from the following
table for each of the U and V directions.
| type |
min # of parameters |
# of control points |
| Taylor |
2 |
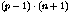 |
| Bézier |
2 |
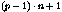 |
| cardinal |
2 |
p + 2 |
| basis matrix |
2 |
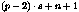 |
| B-spline |
2(n+1) |
p - n - 1 |
Note that only certain numbers of control points are possible;
for example, if the U basis is a degree-3 Bézier, the number
of control points in the U direction can be 4, 7, 10, 13, and so
on, but not 3 or 5. For B-spline
bases of degree 3 the minimum number of parameters is 8
corresponding to 4 control points.
Each vertex reference in the hom_vertex_ref_list is an
integer index into the vertex list of the current group in the
object (index 0 is the first vertex). When the surface is rational,
homogeneous coordinates
must be given with the control points, by appending a floating-point
weight to every vertex reference integer in the
hom_vertex_ref_list. There are two methods for specifying
weights: either a simple floating-point number that must contain a
decimal point to distinguish it from an integer index, or the
keyword w followed by a weight value that need not contain
a decimal point. The w keyword method is recommended
because it eliminates the requirement that numbers contain decimal
points, so translators can use %g format specifiers.
Weights are used only if the surface is rational and ignored
otherwise. If a weight in a rational surface is missing, it
defaults to 1.0.
The surface specials list is used to define trimming curves, hole curves, special curves, and special points (vertex references). A
surface may be further modified by approximation and connection
statements, as described below.
For example, an object with a simple degree-3 Bézier
surface can be written as:
object "mysurface"
visible
basis "bez3" bezier 3
group
0.314772 -3.204608 -7.744229 # vector 0
0.314772 -2.146943 -6.932366
0.314772 -1.089277 -6.120503
0.314772 -0.031611 -5.308641
-0.660089 -2.650739 -8.465791 # vector 4
-0.660089 -1.593073 -7.653928
-0.660089 -0.535407 -6.842065
-0.660089 0.522259 -6.030203
-1.634951 -2.096869 -9.187352 # vector 8
-1.634951 -1.039203 -8.375489
-1.634951 0.018462 -7.563627
-1.634951 1.076128 -6.751764
-2.609813 -1.543000 -9.908914 # vector 12
-2.609813 -0.485334 -9.097052
-2.609813 0.572332 -8.285189
-2.609813 1.629998 -7.473326
v 0 v 1 v 2 v 3 # vertices
v 4 v 5 v 6 v 7
v 8 v 9 v 10 v 11
v 12 v 13 v 14 v 15
surface "surf1" "material"
"bez3" 0.0 1.0 0.0 1.0
"bez3" 0.0 1.0 0.0 1.0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
end group
end object
First, 16 vectors are defined, each of which is used to build
one vertex (control point). Next, a surface is defined that uses
basis bez3 for both the U and V parameter directions.
Since the surface is built from only one 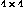 Bézier patch, the parameter vector after the basis range
has only length 2. If there had been two patches in the U direction
and three in the V direction, the bases would have been referenced
as
Bézier patch, the parameter vector after the basis range
has only length 2. If there had been two patches in the U direction
and three in the V direction, the bases would have been referenced
as
"bez3" 0.0 1.0 0.0 0.5 1.0
"bez3" 0.0 1.0 0.0 0.33333 0.66667 1.0
Alternatively, the parameter vector may be given as
"bez3" 0.0 2.0 0.0 1.0 2.0
"bez3" 0.0 3.0 0.0 1.0 2.0 3.0
by changing the parameter
range of the basis. This has no influence on the geometry of
the surface, but generates UV texture coordinates in a different
range (here, 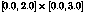 ). However, a different
parameterization does affect the texture surface range (see below),
and the range of trimming, hole, and special curves (which do not
define their own ranges but borrow the range from the surface they
apply to).
). However, a different
parameterization does affect the texture surface range (see below),
and the range of trimming, hole, and special curves (which do not
define their own ranges but borrow the range from the surface they
apply to).
The optional surface_specials_list that completes the
surface definition is a sequence of trimming curves, hole curves,
special curves, and special points as described in the next
section.
Surface Derivatives
mental ray can automatically generate surface derivative vectors if requested. First
derivatives describe the UV parametric gradient of a surface;
second derivatives describe the curvature. They are computed and
stored only if requested by derivative_request statements in
the surface definition:
derivative numberint [ numberint ]
There can be one or more derivative statements that
request first and/or second derivatives. Valid values for
number are 1 and 2, for first and second derivatives,
respectively.
mental ray does not use derivative vectors but makes them
available to shaders. First derivatives are presented as two
vectors (dS du and dS dv, with S being the surface
and the derivatives evaluated at the current point in parameter
space); second derivatives are presented as three vectors (d^2 S
du^2, d^2 S dv^2, and d^2 S du dv). This is the
same format that can be explicitly given for polygonal data using
the d keyword in vertices. Surfaces always compute the
vertex derivatives analytically, explicit vertex derivatives given
by d keywords are ignored.
Texture Surfaces
A plain surface statement defines the geometry of the
surface. If a texture is to be mapped on the surface, it is
necessary to include texture
surfaces. A texture surface defines a mapping from raw UV
coordinates to texture
coordinates as used by shaders. A vector texture is a variation
of a texture surface that additionally defines a pair of basis
vectors; it is used for bump
mapping.
The texture or vector texture directly following a surface
defines texture space number 0,
the next defines texture space number 1, and so on, exactly like
the first t statement after the v statement in a
vertex used for building polygonal geometry defines texture space
number 0, the next t defines texture space number 1, and
so on. Basically, texture and vector texture surfaces replace the
t statements used by polygonal geometry, because attaching
textures to control points that usually are not part of the surface
is not useful.
Texture spaces is what ends up in the 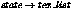 array where it can be accessed by texture
shaders to decide which texture is mapped which way. Texture space
0 is the first entry in that array, which is used by the shader for
the first texture listed in the texture list in the material
definition. In general, there is one texture space per texture on a
material, although shaders making nonstandard use of texture spaces
could be written.
array where it can be accessed by texture
shaders to decide which texture is mapped which way. Texture space
0 is the first entry in that array, which is used by the shader for
the first texture listed in the texture list in the material
definition. In general, there is one texture space per texture on a
material, although shaders making nonstandard use of texture spaces
could be written.
The syntax for texture surfaces is a simplified version of
geometric surfaces. The texture_surface_list in the grammar
summary at the beginning of the "Surfaces" section above expands to
zero or more copies of the following block:
[ volume ] [ vector ] texture
"u_basis_name"u_param_list
"v_basis_name"v_param_list
vertex_ref_list
Unlike geometric surfaces, no surface name and material name is
given. Bases are given like in geometric surfaces. Texture surfaces
use the ranges of the geometric surface they are attached to, they
are not repeated in the texture surface basis statements. The
vertex_ref_list follows the same rules as the geometric
surface's vertex_ref_list. Texture surfaces have no specials
such as trimming curves or holes.
The optional volume keyword in the texture surface
definition disables seam compensation. It should be used for 3D
textures where each texture vector should be used verbatim. If the
volume flag is missing, the tessellator detects textures
that span the geometric seam on closed surfaces, and prevents
rewinding. Consider a sphere with a 2D texture that is shifted
slightly in the U parameter direction: a triangle might have u_0
= 0.0 on one side and u_1 = 0.1 on the other side. If
the texture is shifted towards higher u coordinates by
0.05, u_0 and u_1 will map to texture coordinates t_0 = 0.95
and t_1 = 0.05, assuming an otherwise normal UV mapping.
Even though u_0 < u_1, t_0 >> t_1, causing a
fast "rewind" of the texture. Seam compensation corrects t_1
to 1.05. This is undesirable for 3D textures, which should
have the volume keyword set. Most problems with strangely
shifted textures are caused by inappropriately used or missing
volume keywords.
The optional vector keyword in the texture surface
definition is a flag that causes bump basis vectors to be calculated during
tessellation. This flag must be used if the texture surface is used
for a bump map that expects to find bump basis vectors in the
geometry. However, this is an extremely rare requirement - none of
the standard shaders (base, physics, and contour) or any standard
modeling tool integration shaders require base shaders, so
automatic bump basis vector generation is largely obsolete now. It
was originally introduced for Wavefront compatibility.
This is an example for the simplest of all texture surfaces, a
bilinear mapping:
object "mysurface"
visible
basis "bez1" bezier 1
basis "bez3" bezier 3
group
# ... 16 vectors used for the surface
0.0 0.0 0.0 # vector number 16
0.0 1.0 0.0 # vector number 17
1.0 0.0 0.0 # vector number 18
1.0 1.0 0.0 # vector number 19
# ... 16 vertices used for the surface
v 16 # vertex number 16
v 17 # vertex number 17
v 18 # vertex number 18
v 19 # vertex number 19
surface "surf1" "material"
"bez3" 0.0 1.0 0.0 1.0
"bez3" 0.0 1.0 0.0 1.0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
texture
"bez1" 0.0 1.0
"bez1" 0.0 1.0
16 17 18 19
end group
end object
This texture surface defines a bilinear mapping from the UV
coordinates computed during surface tessellation to the texture coordinates. To define other
than bilinear mappings, the texture surface needs to have more
control points than just one at every corner of the surface.
Whenever the surface tessellator generates a triangle vertex, it
uses the UV coordinate of that vertex to look up the texture
surface and interpolate the texture
coordinate from the nearest four points of the texture surface.
The resulting texture
coordinate is stored with the vertex and becomes available in
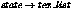 when the
when the
material shader is called because a ray has hit the surface.
If more than one texture surface is given, one texture coordinate is computed for each
texture surface and stored in sequence in the generated triangle
vertices. Each texture surface is said to define a "texture space". They are available
in the 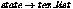 array in the same order. The
number and order of texture surfaces should agree with the number
and order of textures given in the texture list in the material
definition. (Note that not all material shaders support multiple
textures.)
array in the same order. The
number and order of texture surfaces should agree with the number
and order of textures given in the texture list in the material
definition. (Note that not all material shaders support multiple
textures.)
If the material name of a surface is empty (two consecutive
double quotes), the surface uses the material from the closest
instance (this is called material
inheritance).
Curves
Curves are two-dimensional
parametric curves when they are referenced by surfaces. They are
used as trimming curves,
hole curves, and special curves. They must be defined
before the surface which references them. Curves are
three-dimensional parametric curves when referenced by space
curves. A curve is defined as:
curve "curve_name" "basis_name"
parameter_list
hom_vertex_ref_list
[ special special_point_list ]
The parameter_list of a curve is a list of monotonically
increasing floating-point numbers that define the number of
segments of the curve and the number of control points. Curve
parameter lists work very much the same way as surface parameter
lists except that no range needs to be provided, because they are
supplied by the surfaces that reference the curve under
consideration as explained in the next section. For details on
parameter lists, see the sections on bases and surfaces above.
Each vertex reference in the hom_vertex_ref_list is an
integer index into the vertex list of the current group in the
object (index 0 is the first vertex), optionally followed by the
keyword w and a weight value. (For backwards
compatibility, the w keyword may be omitted if the weight
is a floating-point value containing a decimal point.) Weights are
used only if the curve is rational, they are ignored otherwise. If
a weight in a rational curve is missing, it defaults to 1.0. The
vertices indexed by the integers in the hom_vertex_ref_list
should have no normals or textures (no n and t
statements), and the third component of the vector ( v
statement) should be 0.0 because curves are defined in UV
space, not 3D space.
The optional
special_point_list specifies points that are included in the
approximation of the curve. After the special keyword, a
sequence of integers follows that index into the vertex list, just
like the integers in the hom_vertex_ref_list. The first
component of the vector is used as the t parameter; it
forces the point on the curve at parameter value t to become
part of the curve approximation. Of course t must be in the
range of parameters allowed by the surface definition.
Trimming, Hole, and Special Curves; Special Points
A surface may reference curves to trim the surface, to cut holes
into it, and to specify "special curves" that become part of the
tessellation of the surface. Special points in surfaces work like
special points in curves, except that they provide a point in the
parameter range of the surface, that is, a two-dimensional UV
coordinate, rather than a one-dimensional curve parameter. They
specify single points on the surface that are to be included in the
tessellation. As all curves and points are in UV space, the third
component of the vectors provided for them is ignored. None of the
above types of curves and points may exceed the range of (0.0,
1.0) at any point.
No two curves may intersect each other, and no curve may
self-intersect. This is an important point because trimming curves
and holes that are not closing or intersecting themselves or other
loops can produce unexpected tessellation results.
Trimming, hole, and special curves and special points are
defined at the end of the surface definition. The curves are
composed of segments from the list of curves of the surface's
group. The surface_specials_list given in the previous
section is a list of zero or more of the following four
items:
trim "curve_name"min max
...
hole "curve_name"min max
...
special "curve_name"min max
...
special vertexint
...
The dots indicate that each trim, hole, and special statement
may be followed by more than one curve segment or vertex,
respectively. All listed segments are concatenated to form a single
curve.
The vertex integers specify vertices from the vertex
section of the current group in the current object. Such a vertex
specifies the UV coordinate of the special point that is to be
included in the tessellation.
Each of the three types of curves references a curve that has
been defined earlier with a curve statement. If a single
trim, hole, or special statement is
followed by more than one curve, the resulting trimming, hole, or
special curve is pieced together by concatenating the given curves.
The min and max parameters allow using only part of
the curve referenced. min and max must be in the
range of the parameter vector of the curve which in turn must be
mapped into the parameter range
of the surface. The min and max parameters of two
different curve pieces are independent, they only depend on the
curve parameter lists. For example, a trimming curve can be built
from two curves, using the first three quarters of the first curve
and the last three quarters of the second curve:
curve "trim1"
"bez1" 0.0 1.0 2.0 3.0 4.0
0 1 2 3 4
curve "trim2"
"bez1" 0.0 1.0 2.0
3 5 0
surface "patch1" "mtl"
"bez3" 0.0 1.0 0.0 1.0
"bez3" 0.0 1.0 0.0 1.0
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
trim "trim1" 0.0 3.0
"trim2" 0.5 2.0
Both trimming curves use the
basis bez1, which is assumed to be a degree-1 linear
curve. Hence, trim1 connects the UV vertices 0, 1, 2, 3,
and 4 with straight lines, and trim2 connects the vertices
3, 5, and 0. If these two curves are put together by the
trim statement in the surface definition, all parts of the
surface that fall outside the polygon formed by the UV vertices 0,
1, 2, 3, and 5 are trimmed off. The trim2 curve includes
vertex 0 to close the trimming curve. Holes and special curves are constructed exactly
the same way. Trimming curves and holes must form closed loops but
special curves are not restricted in this way.
Note that trimming and hole curves must be listed in the correct
order, outside in. If there is an outer trimming curve, it must be
listed first, followed by the holes. If a hole has a hole, the
inner hole must be listed after the outer hole. Since curves may
never intersect, there is always an unambiguous order - if a curve
A encloses curve B, A must be listed before B. Curves that do not
enclose one another can be listed in any order.
This example omits the vector and vertex parts of the group in
the object. Here is an example that defines a complete object
containing a surface with a trimming
curve that precisely follows the outer boundary. A trimming
curve that follows the outer surface boundary does not actually
clip off any part of the surface, but it is still useful if
surfaces are to be connected, because connections work on trimming
curves.
object "mysurface"
visible
basis "bez1" bezier 1
basis "bez3" bezier 3
group
# ... 16 vectors used for the surface
0.0 0.0 0.0 # vector number 16
1.0 0.0 0.0 # vector number 17
1.0 1.0 0.0 # vector number 18
0.0 1.0 0.0 # vector number 19
# ... 16 vertices used for the surface
v 16 # vertex number 16
v 17 # vertex number 17
v 18 # vertex number 18
v 19 # vertex number 19
curve "trim1"
"bez1" 0.0 0.25 0.5 0.75 1.0
16 17 18 19 16
surface "surf1" "material"
...
trim "trim1" 0.0 1.0
end group
end object
The trimming curve in the example is linear, using a degree-1
Bézier basis. This means that the parameter vector has five equally-spaced
parameters, one for each corner in counter-clockwise order and back
to the first corner to close the trimming curve. Trimming and holes
always require a closed curve or sequence of curves (they can be
pieced together by multiple curves as long as the pieces form a
closed loop together). The results are undefined if trimming or
hole loops are not closed, or intersect.
If the trimming curve would be a degree-3 Bézier going
through four corner points, a parameter vector with 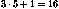 parameters would be required (again, the
5 is the number of corners visited including the return to
the first to close the curve).
parameters would be required (again, the
5 is the number of corners visited including the return to
the first to close the curve).
For details on the parameter vector following the basis name in
the definition of the curve, refer to section curve. The bases and parameter vectors for
curves and surfaces follow the same rules, except that curves have
no explicit range; they always use the implicit range given by the
parameter list.
Connections and Edge Merging
Free-form
surfaces may be connected to each other using the connect
statements, respectively.
The connect statement is "manual" in that it requires
an explicit specification of the parts of two surfaces to be
connected. These parts refer to intervals of trimming curves
or hole curves of these surfaces, see section curve. A connection is defined
as:
connect "surface_name1" "curve_name1" min_1 max_1
"surface_name2" "curve_name2" min_2 max_2
This statement closes the gap between two surfaces
surface_name1 and surface_name2
by connecting their trimming curves curve_name1
and curve_name2. The curves are connected only in
the range (min_1...max_1) and
(min_2...max_2), respectively. They share the same
points, but normals, textures etc. are evaluated on the individual
surfaces. Only surfaces that have trimming curves can be connected
by an explicit connect statement. Trimming curves used in
connections must satisfy three conditions:
- As always, the trimming curve or sequence of trimming curves
must be closed.
- It does not matter whether the trimming curve is oriented
clockwise or counterclockwise, but if a sequence of trimming curves
is used all pieces must have the same direction.
- The trimming curves along the connected range must run in the
same direction in 3D space.
The range values min_1,2 and max_1,2 must not
exceed the range of the trimming curve segment as referenced by a
trim statement of the corresponding surface. The minimum
value must be less than the maximum value; it is not possible to
satisfy the third condition by inverting the range.
Best results are obtained if the curves to be connected are
close to each other in world space and have at least approximately
the same length. The connect statement is not meant to be
a replacement for proper modeling. For carefully modeled surfaces
these techniues will not be necessary most of the time. Their
purpose is to close small cracks between adjacent surfaces that are
already not too far from each other. Topologically complex
situations with several connections meeting in a point are beyond
its scope.
The algorithms
used impose no inherent limit. The limit may be increased in future
versions.
Copyright © 1986-2007 by mental images GmbH
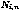 below) to be used in the description of
curves or surfaces. Curves and surfaces reference bases by name.
Every surface needs two bases, one for the U and one for the V
parameter direction. Both can have a different degree, but must
have the same type (for example, rational Bézier in U and
Cardinal in V is not allowed). There are five basis types:
below) to be used in the description of
curves or surfaces. Curves and surfaces reference bases by name.
Every surface needs two bases, one for the U and one for the V
parameter direction. Both can have a different degree, but must
have the same type (for example, rational Bézier in U and
Cardinal in V is not allowed). There are five basis types: . If the curve is of degree n, then
n+1 control points are needed for each polynomial segment.
If the stepsize is given as s, then the
(1+i)th polynomial segment will use the control points
. If the curve is of degree n, then
n+1 control points are needed for each polynomial segment.
If the stepsize is given as s, then the
(1+i)th polynomial segment will use the control points
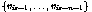 . For example, for Bézier curves
s=n, whereas for Cardinal curves s=1. For surfaces,
the above description applies independently to each parametric
dimension.
. For example, for Bézier curves
s=n, whereas for Cardinal curves s=1. For surfaces,
the above description applies independently to each parametric
dimension.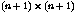 .
The matrix is laid out in the order
.
The matrix is laid out in the order 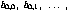
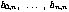 . Note that the generalization to the
rational case for all representations is admitted in all cases.
. Note that the generalization to the
rational case for all representations is admitted in all cases. must have at
least q+1=2(n+1) elements. Knot values represent a monotone
sequence of floating-point numbers but are not necessarily strictly
increasing, i.e.
must have at
least q+1=2(n+1) elements. Knot values represent a monotone
sequence of floating-point numbers but are not necessarily strictly
increasing, i.e. 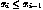 . Moreover, they must
satisfy the following conditions:
. Moreover, they must
satisfy the following conditions: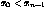 (2)
(2) 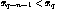 (3)
(3) 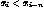 for
for 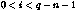 (4)
(4) 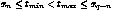
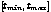 is the range over which the
is the range over which the
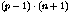
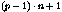
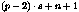
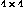 Bézier patch, the
Bézier patch, the 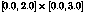 ). However, a different
parameterization does affect the texture surface range (see below),
and the range of trimming, hole, and special curves (which do not
define their own ranges but borrow the range from the surface they
apply to).
). However, a different
parameterization does affect the texture surface range (see below),
and the range of trimming, hole, and special curves (which do not
define their own ranges but borrow the range from the surface they
apply to). array where it can be accessed by texture
shaders to decide which texture is mapped which way. Texture space
0 is the first entry in that array, which is used by the shader for
the first texture listed in the texture list in the material
definition. In general, there is one texture space per texture on a
material, although shaders making nonstandard use of texture spaces
could be written.
array where it can be accessed by texture
shaders to decide which texture is mapped which way. Texture space
0 is the first entry in that array, which is used by the shader for
the first texture listed in the texture list in the material
definition. In general, there is one texture space per texture on a
material, although shaders making nonstandard use of texture spaces
could be written. when the
when the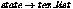 array in the same order. The
number and order of texture surfaces should agree with the number
and order of textures given in the texture list in the material
definition. (Note that not all material shaders support multiple
textures.)
array in the same order. The
number and order of texture surfaces should agree with the number
and order of textures given in the texture list in the material
definition. (Note that not all material shaders support multiple
textures.)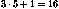 parameters would be required (again, the
5 is the number of corners visited including the return to
the first to close the curve).
parameters would be required (again, the
5 is the number of corners visited including the return to
the first to close the curve).