Approximations
Approximations are defined within an object group and they specify how
previously defined polygons, surfaces, and curves should be
tessellated. Within an object group containing free-form surface
geometry the approximation statements are given separately for the
surface itself and for curves used by the surface. The
surface approximation statement sets the approximation
technique for the surface itself. If it carries a displacement map
this statement refers to the underlying geometric base surface and
does not take the displacement into account. One may specify the
approximation criteria on the displaced surface with an additional
displace approximation statement or even leave out the
surface approximation statement altogether.
If the material of the surface does not contain a displacement
shader the displace approximation statement is ignored. A
trim approximation statement applies to all trimming, hole
and special curves attached to the given surface or surfaces
collectively; it is equivalent to separate curve
approximations for each individual curve. When the keyword
approximate is directly followed by an approximation
technique it refers to a polygon or a list of polygons. It only has
an effect on displacement mapped polygons. If the options statement specifies
approximation statements for base surfaces and/or displacements,
they override the approximation statements in the object. This can
be used for quick previews with low tessellation quality, for
example.
flags approximate
technique [ minint maxint ]
flags approximate surface
technique [ minint maxint ] [ max maxint ] "surface_name" ...
flags approximate displace
technique [ minint maxint ] "surface_name" ...
flags approximate trim
technique [ minint maxint ] "surface_name" ...
flags approximate curve
technique [ minint maxint ] "curve_name" ...
flags approximate space curve
technique [ minint maxint ] "spacecurve_name" ...
The dots indicate that there may be more than one
surface_name or curve_name following the
approximation statement. The given approximation is then used for
all named surfaces or curves. The flags are explained in more
detail in subsection approxflag below.
technique stands for one or more of the following:
view
offscreen
tree
grid
fine3.1
delaunay
[ regular ] parametric u_subdiv [ v_subdiv ]
[ regular ] parametric u_subdiv% [ v_subdiv% ]
any
sharp sharp3.1
length edge
distance dist
angle angle
spatial [ view ] edge
curvature [ view ] dist angle
grading angle
tree, grid, fine, and
delaunay are mutually exclusive. parametric
cannot be combined with any of the others except grid,
which is the default for the parametric case anyway.
regular can only be used together with
parametric. view has no effect unless one of
length, distance, spatial, or
curvature is also given. Grading can only be used in
combination with Delaunay triangulation.
View-dependent approximation is enabled if the
view statement is present. It controls whether the
edge argument of the length and spatial
statements, and the dist argument of the distance
and curvature statements, are in the space the object is
defined in or in raster
space.
Normally geometry outside the viewing frustum is tessellated
much more coarsely because it is not directly visible. However, in
some cases it may become visible due to large flat mirrors, or is
casting shadows on visible geometry. In these cases the
offscreen flag can be used to tessellate geometry outside
the viewing frustum at the full accuracy. Note that this can
generate very large numbers of triangles for things like large
displaced ground planes very close to the camera.
Tree, grid, and Delaunay approximation algorithms are
available for surface approximation. The grid algorithm tessellates
on a regular grid of isolines in parameter space; the tree
algorithm tessellates in a hierarchy of successive refinements that
produces fewer triangles for the same quality criteria; Delaunay triangulation creates a
successive refinement that maximizes triangle equiangularity. By
definition parametric approximations always use the grid algorithm;
all others can use either but tree is the default.
tree, grid, and delaunay have no effect
on curve approximations. Delaunay triangulation creates more
regular triangles but takes longer to compute.
Parametric approximation subdivides each patch of the
surface into u_subdiv 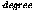 equal-sized pieces in the U parameter direction, and
v_subdiv
equal-sized pieces in the U parameter direction, and
v_subdiv 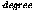 equal-sized pieces in
the V parameter direction. If regular the number of pieces
the whole surface is subdivided into simply equals the parameter
value; the number of subdivisions may also be specified as the
percentage of v_subdiv must be present for surface
approximations and must be omitted for curve and
trim approximations. Note that the factor is a floating
point number, although a patch can only be subdivided an integral
number of times. For example, if a factor of 2.0 is given and the
surface is of degree three, each patch will be subdivided six times
in each parametric direction. If a factor of 0.0 is given, each
patch is approximated by two triangles.
equal-sized pieces in
the V parameter direction. If regular the number of pieces
the whole surface is subdivided into simply equals the parameter
value; the number of subdivisions may also be specified as the
percentage of v_subdiv must be present for surface
approximations and must be omitted for curve and
trim approximations. Note that the factor is a floating
point number, although a patch can only be subdivided an integral
number of times. For example, if a factor of 2.0 is given and the
surface is of degree three, each patch will be subdivided six times
in each parametric direction. If a factor of 0.0 is given, each
patch is approximated by two triangles.
Curves are subdivided in 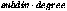 equal
pieces by the parametric approximation and into
subdiv equal pieces by the regular parametric
approximation.
equal
pieces by the parametric approximation and into
subdiv equal pieces by the regular parametric
approximation.
For displacement mapped polygons and displacement mapped
surfaces with a displace statement regular
parametric has the same meaning as parametric in the
approximation. For displacement mapped polygons the u_subdiv
constant specifies that each edge in the triangulation of the
original polygon is subdivided for the displacement 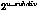 times. If a displace approximation is
given for a displacement mapped surface, the initial tessellation
of the underlying geometric surface is subdivided in the same way
as for polygons. For example, a value of 2 leads to a fourfold
subdivision of each edge. Non-integer values for the subdivision
constant are admissible. Nothing is done if the expression above is
smaller than 2 (if u_subdiv < 1). The
v_subdiv constant is ignored for the parametric
approximation of displacement maps.
times. If a displace approximation is
given for a displacement mapped surface, the initial tessellation
of the underlying geometric surface is subdivided in the same way
as for polygons. For example, a value of 2 leads to a fourfold
subdivision of each edge. Non-integer values for the subdivision
constant are admissible. Nothing is done if the expression above is
smaller than 2 (if u_subdiv < 1). The
v_subdiv constant is ignored for the parametric
approximation of displacement maps.
Length/distance/angle (LDA) approximation specifies
curvature-dependent approximation according to the criteria
specified by the length, distance, and
angle statements. These statements can be given in any
combination and order, but cannot be combined with parametric
approximation in the same approximate statement. If they
are preceded by the any keyword the approximation stops as
soon as any of the criteria is satisfied.
The length statement subdivides the surface or curve
such that no edge length of the tessellation exceeds the
edge parameter. edge is given as a distance in the
space the object is defined in, or as a fraction of a pixel
diagonal in raster space if the
view keyword is present. Small values such as 1.0 are
recommended. For tree and grid approximation the min and
max parameters, if present, specify the minimum and maximum
number of recursion levels of the adaptive subdivision. The
min parameter is a means to enforce a minimal triangulation
fineness without any tests. Edges are further subdivided until they
satisfy the given criterion is fulfilled or the max
subdivision level is reached. The defaults are 0 and 5,
respectively; 5 is a very high number. mental ray imposes a hard
maximum of 7; mental ray 3.3 and higher have no hard limit for
displacement. Good results can often be achieved with a maximum of
3 subdivisions. For Delaunay approximation, the number max
following the keyword max specifies the maximum number of
triangles of the surface tessellation. This number will be exceeded
only if required by trimming, hole, and special curves because
every curve vertex must become part of the tessellation regardless
of the specified maximum.
For displacement mapped polygons and displacement mapped
surfaces with a displace approximation statement the
length criterion in the approximation limits the size of the edges
of the displaced triangles and ensures that at least all features
of this size are resolved. Subdivision stops as soon as an edge
satisfies the criterion or when the maximum subdivision level is
reached. It cannot be ruled out that at an even finer scale new
details may show up which would lead again to longer edges. This
caveat about the potential miss of high-frequency detail applies
also to the distance and angle criteria.
The distance statement specifies the maximum distance
dist between the tessellation and the actual curve or
surface. The value of dist is a distance in the space the
object is defined in, or a fraction of a pixel diagonal in raster space if the view
statement is present. As a starting point, a small distance such as
0.1 is recommended. For tree and grid approximation the min
and max parameters, if present, specify the minimum and
maximum number of recursion levels of the adaptive subdivision. For
Delaunay approximation, the number max following the keyword
max specifies the maximum number of triangles of the
surface tessellation.
For displacement mapped polygons and displacement mapped
surfaces with a displace approximation statement the
distance criterion cannot be used in the same way because the
displaced surface is not known analytically. Instead, the
displacements of the vertices of a triangle in the tessellation are
compared. The criterion is fulfilled only if they differ by less
than the given threshold. Subdivision is finest in areas where the
displacement changes. For example, if a black-and-white picture is
used for the displacement map the triangulation will be finest
along the borders between black and white areas but the resolution
will be lower away from them in the uniformly colored areas. In
such a case one could choose a moderately dense parametric
surface approximation that samples the displacement map at
sufficient density to catch small features, and use the
curvature-dependent displace approximation to resolve the
curvature introduced by the displacement map. Even if the base
surface is triangulated without adding interior points, as if its
trim curve defined a polygon in parameter space, it is still
possible to guarantee a certain resolution by increasing the
min subdivision level. Only the consecutive subdivisions are
then performed adaptively.
The angle statement specifies the maximum angle
angle in degrees between normals of adjacent tiles of a
displaced polygon or the tessellation of a surface or its
displacement or between tangents of adjacent segments of the curve
approximation. Large angles such as 45.0 are recommended. For tree
and grid approximation the min and max parameters, if
present, specify the minimum and maximum number of recursion levels
of the adaptive subdivision. For Delaunay approximation, the number
max following the keyword max specifies the maximum
number of triangles of the surface tessellation.
Spatial approximation as specified by a spatial
statement is a special case of an LDA approximation that specifies
only the length statement. For backwards compatibility,
the spatial statement has been retained; it is equivalent
to the length statement plus an optional view
statement.
Curvature-dependent approximation as specified by the
curvature statement is also a special case of LDA
approximation, equivalent to a distance statement, an
angle statement, and an optional view statement.
The spatial and curvature statements can be
combined, but future designs should use length,
distance, and angle directly.
Grading applies only to Delaunay triangulation controls the
density of triangles around the border of the surface. It allows
the density of triangles to vary quickly in a smooth transition
between a finer curve approximation and a coarser surface
approximation. The angle constant specifies a lower bound
related to the degree of the minimum angle of a triangle. Values
from 0.0 to 30.0 can be specified. Small values up to 20.0 are
recommended. The default is 0.0. When using high grading values it
is recommended to specify a maximum number of triangles because
otherwise high grading values might result in a huge number of
triangles or endless mesh refinement. The purpose of this option is
to prevent a large number of tiny triangles at the trimming or
hole curve to abruptly join very
large triangles in the interior of the surface.
The sharp3.1 keyword controls the
sharp approximation of
normal vectors. If set to 0.0,
mental ray uses the interpolated normal as specified by the base
surface, modified by displacement if available. If the argument
sharp is set to 1.0, mental ray will use the geometric
normal for a faceted look. This is primarily useful in
fine mode. mental ray 3.2 allows any sharp value
between 0.0 and 1.0; earlier versions distinguish only exactly 0.0
and 1.0.
If no approximation statement is given the parametric technique
is used by default with u_subdiv = v_subdiv = 0 for
surfaces, or u_subdiv = 0 in the case of curves and
polygons.
The following exceptions apply to subdivision surfaces:
- The displace approximation is ignored, and the regular
approximation is used. Subdivision surfaces are refined during
displacement in a single integrated pass, so the separation between
base surface and displaced surface does not apply.
- There are no restrictions on the approximation techniques in
fine mode. Any LDA mode may be used.
Fine Approximations3.1
Standard approximations as described in the
previous section work under the assumption that as few triangles as
possible should be used to approximate a surface to achieve a
user-defined quality. mental ray 3.1 also supports a new
approximation mode called fine approximation, which
addresses the problem from a different angle: it is capable of
efficiently expending very large numbers of triangles to faithfully
approximate even very complex surfaces, especially displaced
surfaces, without excessive memory consumption.
This is done by reducing the granularity of mental ray's cache
manager. In mental ray 3.0, it operated on entire objects, which
could become very large when tessellated. mental ray 3.1 applies
cache management to smaller units formed by splitting objects into
smaller sets, which can be individually tessellated without
excessive memory requirements. This is especially useful for
extremely detailed displacement maps.
Fine approximations support a small subset of approximation
techniques since the remainder exists only to trade off triangle
counts vs. quality, which is no longer a problem for fine
approximations:
fine [ nosmoothing3.4 ]
[ sharp sharp ] 3.1
[ view ] length edge
parametric u_subdiv v_subdiv
The fine keyword enables fine approximation. It can be
used for polygon displacement, free-form surface displacement,
subdivision surface displacement and free-form surface
approximations, but not for curves. fine nosmoothing can
be used for polygon displacement for turning off a smoothing
procedure which is used by default during fine polygon
displacement. As with standard approximations, the sharp
keyword controls normal-vector calculations. If set to 0.0, mental
ray uses the interpolated normal as specified by the base surface,
modified by displacement if available; if set to 1.0, mental ray
will use the geometric normal to achieve a sharp faceted look.
[12]
Fine approximation requires the choice of one of three
techniques:
- view length specifies that all triangles should be
subdivided until they are smaller than edge pixel diagonals.
The edge value is typically around 0.5, or 0.25 or even 0.1
for very high quality. This technique is recommended for all fine
approximations.
- length specifies that the triangle edge length should
stay under edge units in the object's object space. The edge parameter
needs more careful tuning than in the view-dependent case, and very
high values defeat the purpose of fine approximation.
- parametric [13] tessellates
a free-form surface such that all microtriangles have the same
size. This results in very regular meshes but is harder to
optimize, and may use significantly more memory.
This simplicity makes it very easy to control fine displacement,
without the risk of accidentally creating billions of triangles
until memory runs out, and without juggling a large number of
temperamental displacement-mapping parameters.
However, fine displacement critically depends on the
specification of a cache size limit, because otherwise the fine
tessellation results would not flow through the cache but
accumulate until memory runs out. The default cache limit
(unlimited) can be overridden with the -jobmemory (3.0,
3.1) or -memory (3.2 and up) command-line option. A good
choice is 100 MB less than the maximum allocatable memory on 32-bit
machines. If the number is too large, the operating system may run
out of virtual address space; if it is too small, mental ray will
perform too many cache flush operations.
If fine is used to approximate displaced geometry, it is
also important to specify a correct max displace value. This
parameter specifies the maximum absolute scalar value a
displacement shader may return and serves to give mental ray a hint
of the maximum extension of the displaced object. It is measured in
object space. This parameter is
somewhat "sensible": if chosen too large, it may affect rendering
performance; if chosen too small, any larger values returned by a
displacement shader will be clipped. mental ray issues a warning
message if max displace is chosen too small and a greater
value is returned by the shader during rendering, thus providing a
way to adjust max displace optimally. mental ray relies on
max displace exclusively; if accidentally left at the default of
zero, all displacement will disappear (with a warning message).
Fine approximation cannot be used together with merging and
connections.
Flagged Approximations
mental ray 3.2 allows flagged approximations. An
object or instance may optionally prefix approximate
statements with one or more of the flag keywords visible,
trace, shadow, caustic, and
globillum. The approximation then applies only if the
object is hit by the corresponding ray or photon. If no flags are
given, the approximation applies to all rays and photons, which is
equivalent to specifying all five flags. For example,
visible approximate fine view length 0.5 ...
trace shadow approximate regular parametric 3 3 ...
visible approximate displace fine view length 0.25 ...
specifies that where the object is visible to primary rays, it
will be fairly detailed (fine view length 0.5), but its
reflections, refractions, and shadows are very coarse (regular
parametric 3 3). Visible displacements are even finer (fine view
length 0.25). In particular, final gathering falls under
trace, and will also be coarsely approximated. In this
example, mental ray will tessellate the object twice, once for
visible and once for trace shadow. Missing
approximations, in this example for caustic and globillum, use the
default parametric 0 0. The trace flag also applies to final gathering and probe rays
(mi_trace_probe).
The intended use is for simple stand-ins. If the scene contains
many detailed visible objects, it is undesirable to use the same
level of detail for trace objects to compute shadows or global
illumination because those rays are far less coherent, and pull in
far more objects into the geometry cache simultaneously. Hence,
simpler stand-ins should be used. This can be done by specifying
entire separate objects with visible and trace
object flags, but it is simpler to use the same objects and
applying the flags only to the approximations.
Since low-resolution shadow and trace stand-in objects are
usually a small distance offset from the high-resolution visible
object, it is often useful to offset rays at least that distance
away from the visible object, using mi_ray_offset in the shader.
mental ray 3.1.
supports only the two modes sharp 1.0 (faceted look) and sharp 0.0
(default); mental ray 3.2 and higher support any value between 0.0
and 1.0.
Parametric
approximation is supported only for free-form surfaces and not for
displaced geometry.
Copyright © 1986-2007 by mental images GmbH
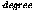 equal-sized pieces in the U parameter direction, and
v_subdiv
equal-sized pieces in the U parameter direction, and
v_subdiv 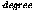 equal-sized pieces in
the V parameter direction. If regular the number of pieces
the whole surface is subdivided into simply equals the parameter
value; the number of subdivisions may also be specified as the
percentage of v_subdiv must be present for surface
approximations and must be omitted for curve and
trim approximations. Note that the factor is a floating
point number, although a patch can only be subdivided an integral
number of times. For example, if a factor of 2.0 is given and the
surface is of degree three, each patch will be subdivided six times
in each parametric direction. If a factor of 0.0 is given, each
patch is approximated by two triangles.
equal-sized pieces in
the V parameter direction. If regular the number of pieces
the whole surface is subdivided into simply equals the parameter
value; the number of subdivisions may also be specified as the
percentage of v_subdiv must be present for surface
approximations and must be omitted for curve and
trim approximations. Note that the factor is a floating
point number, although a patch can only be subdivided an integral
number of times. For example, if a factor of 2.0 is given and the
surface is of degree three, each patch will be subdivided six times
in each parametric direction. If a factor of 0.0 is given, each
patch is approximated by two triangles.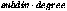 equal
pieces by the parametric approximation and into
subdiv equal pieces by the regular parametric
approximation.
equal
pieces by the parametric approximation and into
subdiv equal pieces by the regular parametric
approximation.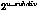 times. If a displace approximation is
given for a displacement mapped surface, the initial tessellation
of the underlying geometric surface is subdivided in the same way
as for polygons. For example, a value of 2 leads to a fourfold
subdivision of each edge. Non-integer values for the subdivision
constant are admissible. Nothing is done if the expression above is
smaller than 2 (if u_subdiv < 1). The
v_subdiv constant is ignored for the parametric
approximation of displacement maps.
times. If a displace approximation is
given for a displacement mapped surface, the initial tessellation
of the underlying geometric surface is subdivided in the same way
as for polygons. For example, a value of 2 leads to a fourfold
subdivision of each edge. Non-integer values for the subdivision
constant are admissible. Nothing is done if the expression above is
smaller than 2 (if u_subdiv < 1). The
v_subdiv constant is ignored for the parametric
approximation of displacement maps.