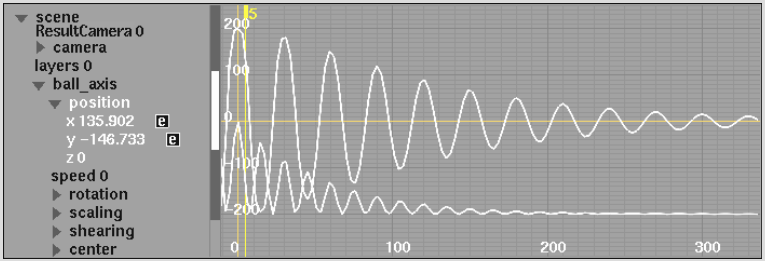
To see this example, load the setup named expressions_dampened_pendulum into Action. This examples involves a pendulum (a ball attached to a rope) that swings freely back and forth under the force of gravity until it comes to a stop.


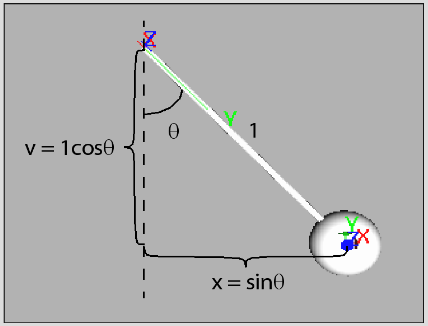
The ball oscillates in a dampened harmonic motion that is created by animating the position of the ball and the rotation of the rope. The ball's x position is defined as the sine of the swing angle between the rope and centre axis, multiplied by the length of the rope. This angle is initially PI/2 and decreases logarithmically. In addition, the ball oscillates with a period of 30 frames. The sin function is used to calculate the sine of the swing angle and the exp function is used to create the logarithmic dampening effect. The cos function is used to create the oscillation.
The ball's y position is defined as the negative cosine of the swing angle between the rope and centre axis, multiplied by the length of the rope. This expression is formed similarly to that of the ball_axis.position.x channel. The rope rotates such that its Y-axis is always pointing toward the centre of the ball. The lookat function is used to generate the rotation vector.
| Channel | Expression |
|---|---|
| ball_axis.position.x | sin(PI / 2 / exp(frame / 100) * cos(frame * 2 * PI / 30)) *200 |
| ball_axis.position.y | -cos(PI / 2 / exp(frame / 100) * cos(frame * 2 * PI / 30))* 200 |
| rope_axis.rotation | lookat(ball_axis.position, rope_axis.position, (0,1,0), (0,0,1)) |