
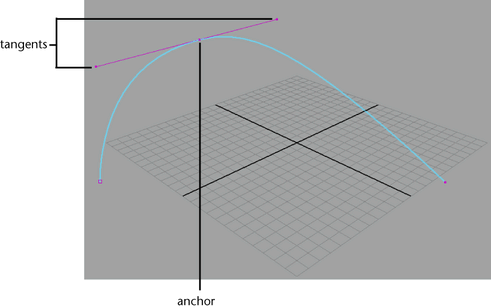
Bezier curves are a subset of NURBS curves that are composed of two types of control vertices, anchors and tangents. Anchors lie on the curve and determine the origin of tangents. Tangents determine the shape of the curve leading to an adjacent anchor.
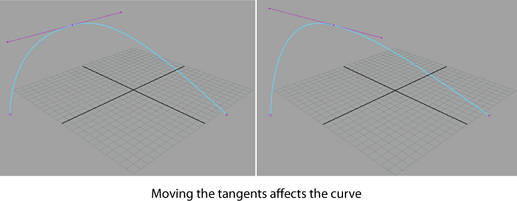
Since Bezier curves are a subset of NURBS curves, you can perform the majority of NURBS operations to Bezier curves as well. You can also perform NURBS operations on combinations of Bezier curves and NURBS curves. In general, an operation involving all Bezier curves results in a Bezier curve while operations involving a combination of Bezier and NURBS curves results in a NURBS curve.
Mathematics behind Bezier curves
All Bezier curves in Maya are cubic, meaning a curve between two anchors is determined by four points, p1 to p4.
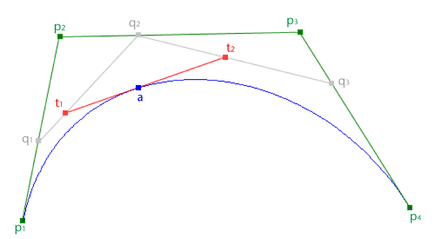
The curve starts at p1 and moves towards p2 before it arcs toward p4 by way of p3.
At any point, you can find the position of anchor a from the following equation:
a(x) = (1-x)3P1 + 3(1-x)2xP2 + 3(1-x)x2P4
Where x is any value greater or equal to 0, and less than or equal to 1.
Mathematically, a Bezier curve is built by plotting a point for every value of x and then connecting those points. In Maya, you can draw a Bezier curve by plotting anchors and adjusting the tangents (t1 and t2) manually.