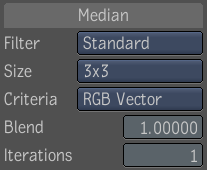
The Median tool is an edge-preserving smoothing filter that works particularly well for removing impulse noise.
For grayscale images, the median filter works by ranking the pixels under the kernel according to their value and selecting the median to replace the pixel at the center of the kernel. This approach effectively removes spikes in the original image without the blurring typically introduced by common smoothing kernels (e.g. Gaussian).
For color images, there is no single concept of ranking, so several different criteria are supported. Component-wise ranking computes the median of each color component independently, however, this can result in pixel colors that did not belong in the original image. Luminance ranking computes the median of the luminance of each pixel under the kernel. This approach is fast and does not introduce new colors in the original image, however, luminance is not the best criteria for similarity in a color image. RGB Vector does not really rank the pixels under the kernel, but rather it chooses as the median the one pixel with the smallest sum of square distances (in RGB space) to all the other ones under the kernel. It selects the pixel that is closest to the center of the point cloud obtained by looking at the pixels under the kernel as points in 3D space. This approach is computationally intensive, but can yield better results than either of the other ranking criteria.
The median filter uses a square neighborhood and can round the corners of axes-aligned rectangular objects in an image.
As any noise reduction filter, the median filter may also affect the sharpness of small details in the input image. When this problem arises, the result of the median filter can be blended with the original image to decrease its effect.
Finally, the median filter can be applied recursively. Repeated applications using a small kernel size yield better results than a single application using a large kernel.
The Median tool has the following parameters: