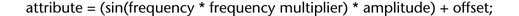Returns the sine of an angle specified in radians.
number is the angle, in radians, whose sine you want.
For any right triangle, the sine of an angle is the following ratio:
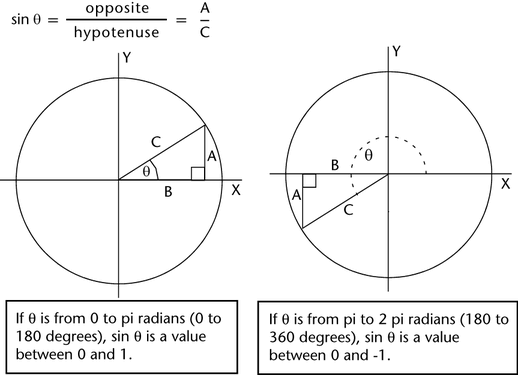
The sine ratio depends only on the size of the angle and not on the size of the triangle. This constant ratio is called the sine of the measure of the angle.
The sine ratio is a value between -1 and 1.
With a steadily increasing or decreasing argument, the sin function returns steadily increasing or decreasing values between -1 and 1. This is useful for creating rhythmic, oscillating changes in attribute values.
For example, you can use the sin function to manipulate:
Ball.translateY = sin(Ball.translateX);
This statement sets Ball’s translateY attribute equal to the sine of its translateX attribute. If you drag Ball along the X-axis, Ball’s translateY position moves up and down in a cyclical pattern:
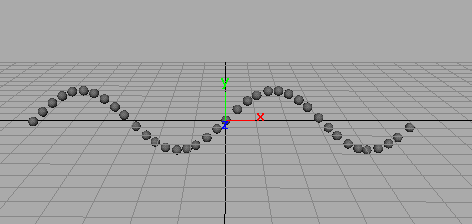
To animate Ball to the path of the preceding example, use this expression:
Ball.translateX = time;
Ball.translateY = sin(Ball.translateX);
Ball starts at the origin and moves in the X direction at a rate set by the incrementing animation time. Its Y translation moves cyclically up and down according to the return values of the sin function. The sin function uses translateX, and therefore indirectly, time, as its argument.
As time increases from 0 to 6.283 seconds, the sin function returns values that change in fine increments from 0 to 1 to -1 to 0. The value 6.283 is 2 times the value of pi. The resulting motion resembles a horizontal S-shape:
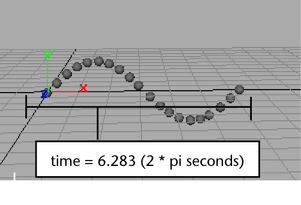
As time increases beyond 6.283 seconds, the same S-shaped cycle repeats for each span of 6.283 seconds.
This expression animates Ball with larger up and down swings:
Ball.translateX = time;
Ball.translateY = sin(Ball.translateX) * 2;
By multiplying sin(Ball.translateX) by a number greater than 1, you increase the amplitude of the sine wave pattern. The amplitude is half the distance between the minimum and maximum values of the wave.
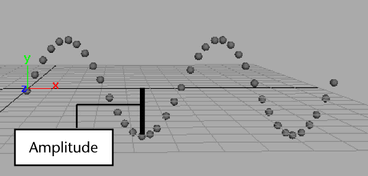
You can decrease the amplitude of the sine wave by multiplying by a number less than 1, for example, 0.5.
This expression increases how often the sine wave completes a cycle:
Ball.translateX = time;
Ball.translateY = sin(Ball.translateX * 2);
By multiplying Ball.translateX by a number greater than 1, you increase the frequency of the sine wave pattern. The frequency is how long it takes the wave to make a complete cycle.
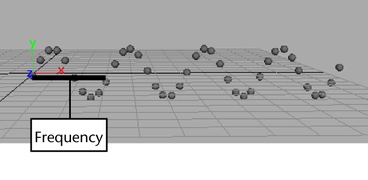
You can decrease the frequency of the sine wave by multiplying by a number less than 1, for example, 0.5. This number is known as a frequency multiplier because it multiplies (or divides) the frequency of the sine pattern.
This expression offsets the wave pattern higher up the Y-axis:
Ball.translateX = time;
Ball.translateY = sin(Ball.translateX) + 2;
By adding 2 to sin(Ball.translateX), the wave pattern starts further up the Y-axis. You can, of course, also subtract a number to offset the wave pattern lower on the Y-axis.

The following expression sets a frequency multiplier, amplitude, and offset of a sine pattern in a single statement:
Ball.translateX = time;
Ball.translateY = (sin(Ball.translateX * 2) * 2) + 2;

The following diagram shows which values set the frequency multiplier, amplitude, and offset.
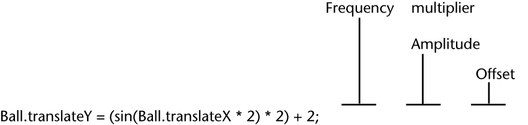
A general equation showing the factors you can use to create a sine wave pattern follows: