CVs

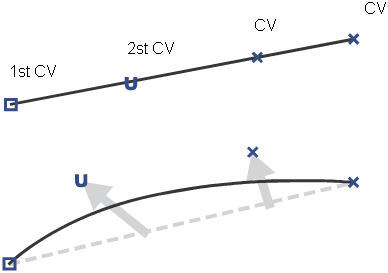
CVs (control vertices) control how the curve is “pulled” from a straight line between edit points. They are the most basic and important means for controlling the shape of a curve. Lines between consecutive CVs form the control hull.

You cannot add CVs to the interior of a curve: there is always a set number of CVs for each span. The number of CVs is equal to the degree of the curve plus one. So, for example, a degree 3 curve has four CVs per span.

Alias draws CVs differently to let you tell the difference between the start and the end of a curve. The first CV (at the start point of the curve) is drawn as a box. The second CV is drawn as a small “U”, to show the increasing U dimension from the start point. All other CVs are drawn as small Xs.

Multiple spans

Longer and more complex curves require more than a single span curve. As you draw what appears to be a single long curve, Alias is actually adding several curve spans together. The last CV of the previous curve span become the first CV of the next curve span, creating very smooth transitions between the curve segments.

Edit points

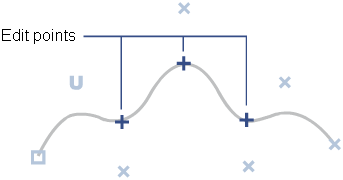
You can tell when a curve is made from multiple spans in several ways. One is to look for edit points on the curve. Edit points mark the connection point between two spans. Alias draws edit points as small crosses.

Unlike the on-curve control points of Bezier curves (used in many 2D illustration programs), NURBS edit points are not usually used for editing curves. CVs control the shape of a NURBS curve, and edit points are just indicators of how many spans a curve has.

There are, however, a few tasks that use edit points:

• If you want more control in a curve, you can insert an edit point to increase the number of spans in the curve and give you more CVs to work with.
• You can also delete edit points to decrease the number of spans in a curve (and probably change the shape of the curve).
• It is possible to move edit points to change the shape of a curve, but avoid doing this except for minor adjustments.

  Alias does not actually move the edit point itself, but instead moves the CVs to reshape the curve so the edit point is where you specified.

Hulls

As a curve gets more spans/edit points, you might lose track of the order of the CVs. To show the relationship between CVs, Alias can draw lines between them. These lines are called hulls.

(Alias also provides other feedback to show the order of CVs. For example, when you pick a CV, Alias highlights its span within the curve.)