Parameters are the unique numeric values (like a coordinate) of points on a curve or surface.
You can think of a curve as made up of an infinite number of points. Each of these that make up a curve has a number, called its parameter. Parameters let you refer to specific points along the length of a curve. The higher the parameter, the further is the point along the curve.
Just as points in space have three dimensions, called X, Y, and Z, the parameters of a point are measured along the one internal dimension (length) of the curve. We call this dimension U.
Since surfaces have two internal dimensions (length and width), we need another parameter (in addition to U) to specify a point on a surface. We call this parameter V.
Just as every point along the length of a curve has a U parameter, every point across a surface has a pair of U and V parameters.

The method Alias uses to number the points along a curve is called the parameterization of the curve. Alias has two parameterization methods: uniform and chord-length.
Each method has advantages and disadvantages depending on how the curve is used. You can choose which parameterization method to use when you create a curve, and you can rebuild existing curves to use a specific parameterization.
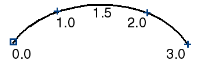
Uniform parameterization assigns integral parameter values to the edit points, and evenly distributes parameters along the spans between edit points. So the first edit point is always parameter 0.0, the second edit point is always 1.0, the third is always 2.0, and so on.
A bonus feature of uniform parameterization is that the parameter value of the last edit point is the also the number of spans in the curve. However, unlike chord-length parameterization, the parameters of a uniform curve have nothing to do with the actual length of the curve.
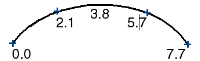
Chord-length parameterization assigns parameter 0.0 to the start of the curve, then increases the parameter value proportionally to the chord length, or the shortest linear distance, between the surrounding edit points.
Unlike uniform parameterization, the parameters of a chord-length curve are irregularly spaced between the edit points, and the edit points do not have integral parameters.
Each parameterization method has advantages and disadvantages, depending on how you use the curve or surface.
| Type | Pros | Cons |
|---|---|---|
| Chord-length | Parameter value gives some indication of the relative position of the point along the curve. Minimizes stretching and squeezing of textures. | Parameters are not obvious. Surfaces built from chord-length curves can be more complex because of cross-knot insertion. |
| Uniform | Easy to reckon parameters (for example, 1.5 is about half-way between edit points at 1.0 and 2.0). | In many cases, interpolation between edit points is not as good. Can lead to unpredictable stretching of textures during rendering. |
Just as with degree, surfaces can have different parameterization methods for their U and V dimensions. For example, the U isoparms of a surface can be degree 3 with uniform parameterization, while the V isoparms are degree 1 with chord-length parameterization.