Parameterization

NURBS are parameterizable, which means that any point along a NURBS can be mathematically defined by one or more parameters.

Curves are defined by a single U parameter along their length; you can describe any point along a curve in terms of its U parameter.

Similarly, surfaces are defined by both U and V parameters; you can describe any point along a curve in terms of its (U, V) coordinates.

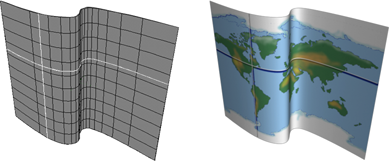
U and V are similar to latitude and longitude.

Depending on how a NURBS is parameterized, different values of U and V correspond to different points. You can reparameterize curves as described in Reparameterizing Curves , and surfaces as described in Reparameterizing Surfaces. Surfaces can have one parameterization type along U and a different one along V.

There are four parameterization methods available:

• With uniform parameterization, the difference between successive knots is the same, regardless of the actual length of the curve segment.

  Uniform parameterization is especially suitable when merging and lofting.

  While it may seem strange that non-uniform rational B-Splines can have a uniform parameterization, it is not a contradiction; "non-uniform" here means "not necessarily uniform."

• With non-uniform parameterization, the difference between successive knots can be anything.

• With chord length parameterization, the difference between successive knot values is related to the actual length of each segment.

  If you could see the knot values on the actual curve, these values might be unequal: 1, 3.2, 5.3, and so on. This is particularly useful when using bitmapped textures.

• With centripetal parameterization, the knot spacing is related to the square root of the length of each curve segment. In some cases, this may make smoother objects. On surfaces of very unevenly spaced control points, it may give slightly better texture mapping results than chord length.

Normally, when you create a NURBS object, its parameterization is uniform. However, that may change and become non-uniform as you perform modeling operations on it.