One essential concept that a first-time user of 3D computer graphics should understand is the notion of working within a virtual three-dimensional space using a two-dimensional user interface.
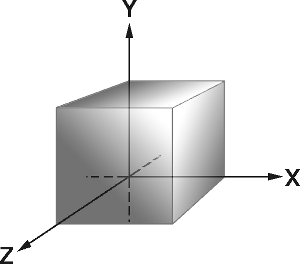
Softimage uses the classical Euclidean/Cartesian mathematical representation of space. The Cartesian coordinate system is based on three perpendicular axes, X, Y, and Z, intersecting at one point. This reference point is called the origin. You can find it by looking at the center of the grid in any of the 3D windows.
To remember the direction of the X, Y, Z axes, use the "right-hand" rule: hold up your right hand so that your palm is facing you, then extend your thumb to the right, hold your index finger up, and point your middle finger towards you. Your thumb is pointing in positive X, your index finger in positive Y, and your middle finger in positive Z. The opposite directions represent negative X, Y, and Z.
A small icon representing the three axes and their directions is shown in the corner of 3D views. The icon's three axes are represented by color-coded vectors: red for X, green for Y, and blue for Z.
With the Cartesian coordinate system, you can locate any point in space using three coordinates. Positions are measured from a point called the origin, which is (0, 0, 0). For example, if X = +2, Y = +1, Z = +3, a point would be located to the right of, above, and in front of the origin.
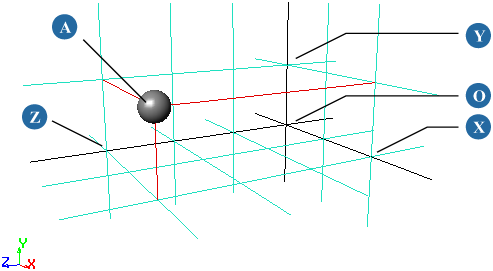
A sphere at a location of (2, 1, 3) (A) is at the intersection of X = 2 (X), Y = 1 (Y), and Z = 3 (Z). Global locations are measured from the origin (O).
Since you are working with a two-dimensional interface, spatial planes are used to locate points in three-dimensional space.
The perpendicular axes extend as spatial planes: XZ, XY, and YZ. In the 3D views, these planes correspond to three of the parallel projection windows: Top, Front, and Right.
Imagine that the XZ, XY, and YZ planes are folded together like the top, front, and right side of a box.
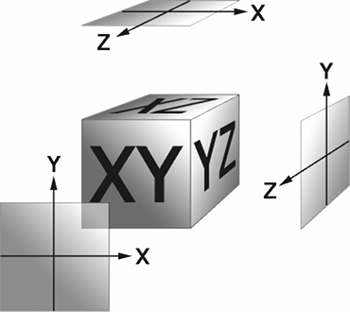
This helps you keep a sense of orientation when you are working within the parallel projection windows.